2017-06-05のアーカイブ

符号付き算術演算のオーバーフロー検出アルゴリズム

インテル8080にオーバーフローフラグが無い

2017年6月、35年ぶりにインテル8080マイクロプロセッサのアセンブラを書いています。

CP/Mシミュレータで懐かしのインテル8080アセンブラを使う

信号処理などでは、サチュレート(飽和)演算を使うことがあります。サチュレート演算とは、演算結果が上限を超えたら上限値に、下限を超えたら下限値にするものです。すなわち、オーバーフローを検出して演算結果を補正するわけです。

信号処理を得意とするDSP(Digital Signal Processor)では、命令セットにサチュレート演算があります。また、マルチメディア対応のSIMD(Single Instruction Multiple Data)命令にも、サチュレート演算命令があります。

しかし、1974年に登場したインテル8080マイクロプロセッサには、残念ながらサチュレート演算命令は存在しません。その上、オーバーフローを検出するオーバーフローフラグもありませんでした。

そこで、ソフトウェアでオーバーフロー検出するアルゴリズムを整理しました。

数値の表現方法

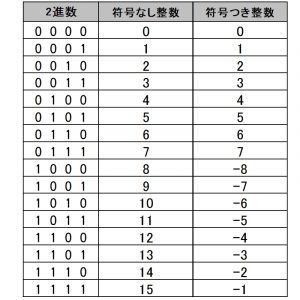
コンピュータ内部は、数値を２進数で格納しています。説明を簡単にするために、ここでは４ビットで説明します。

４ビットの場合、16種類の0と1の組み合わせがあります。

  • 符号なし整数　：　0～15を表します
  • 符号つき整数　：　0～7、-1～-8を表します
4ビット 2進10進数対応表

4ビット 2進10進数対応表

符号つき整数の場合、マイナスの値は「2の補数表現」を使います。「2の補数表現」では、最上位ビット(MSB : Most Significant Bit)が「1」のときマイナス数値を表します。
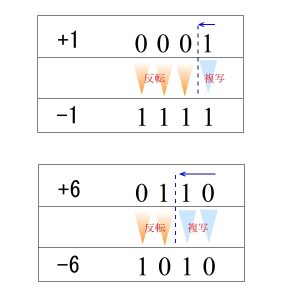
２進数のマイナス数値は、２進数ビット列を反転して+1を加算したものです。

たとえば、

  • 「－１」: 「１ (0001)」を反転した「1110」に+1を加算 → (1111)
  • 「－６」: 「６ (0110)」を反転した「1001」に+1を加算 → (1010)

もっと簡単な手順は、最下位ビットから（右→左へ）順にビット複写して、ビット値１を複写した後はビット反転したものです。

負の数　作成方法

負の数　作成方法

 

２進数のマイナス数値を「2の補数表現」とすることにより、２進数の加算で減算を行うことができます。
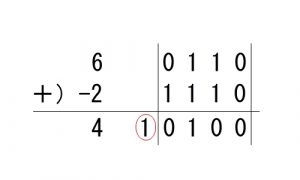
たとえば、「６－２」の計算は「６」と「－２」を加算します。「６(0110)」と「－２(1110)」を加算すると「10100」となります。最上位ビットからはみ出した「1」は、キャリービットと呼び無視します。その結果、計算結果は「４(0100)」となります。

2進数の加算

2進数の加算

 

サチュレート(飽和)演算とは

サチュレート演算とは演算結果がオーバーフローしたら上限値または下限値に補正する演算です。オーバーフローとは、2の補数で表現可能な範囲に収まらないことを言います。

４ビットで説明します。2の補数で表現可能な数値は、最大値は＋７で最小値は－８です。

  • 最大値(＋７)を上回ったら、上限値(＋７)に補正
  • 最小値(－８)を下回ったら、下限値(－８)に補正

 

(+５)＋(+１) 0101＋0001 ＝ 0 0110 ＋６
(+５)＋(+４) 0101＋0100 ＝ 0 1001 オーバーフロー ＋７
(-５)＋(-１) 1011＋1111 ＝ 1 1010 －６
(-５)＋(-４) 1011＋1100 ＝ 1 0111 オーバーフロー －８

 

オーバーフローの検出方法

さて、オーバーフローはどのように検出したらよいか考えてみます。

2の補数表現

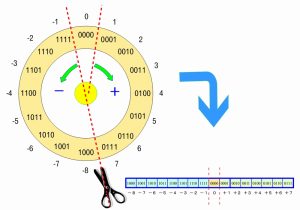
４ビット符号つき整数(2の補数表現)のビットパターンと１０進数数値を下記のように円形で示します。

4ビット符号つき整数

4ビット符号つき整数

  • 「０(0000)」から右回りがプラス方向です。+１～+７。
  • 「０(0000)」から左回りがマイナス方向です。－１～－８。

「＋７(0111)」と「－８(1000)」の間は、連続性が無く円が途切れます。この部分で円弧を切断して、直線状に延ばして計算尺に見立てます。

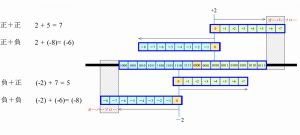
数値の加算

数値Ｂと数値Ｃを加算します。

下記図で、中央に示した計算尺の数値Ｂと、上または下に示した直線の数値Ｃを加算するとします。

4ビット2進数の加算とオーバーフロー

4ビット2進数の加算とオーバーフロー

正の数＋正の数

２＋５は、中央の計算尺の(＋２)と数値(＋５)を加算して(0111)となります。しかし、２＋６は正の最大値(0111)を上回りオーバーフローします。

正の数＋負の数

２＋(-８)は、中央の計算尺の(＋２)と数値(－８)を加算すると(1010)＝(－６)となります。正の数(０～７)に負の数(－１～－８)を加算しても、オーバーフローすることはありません。

負の数＋正の数

(－２)＋７は、中央の計算尺の(－２)と数値(＋７)を加算すると(0101)＝(＋５)となります。負の数(－１～－８)に正の数(０～７)を加算しても、オーバーフローすることはありません。

負の数＋負の数

(－２)＋(－６)は、中央の計算尺の(－２)と数値(－６)を加算して(1000)となります。しかし、(－２)＋(－７)は負の最大値(1000)を下回りオーバーフローします。

オーバーフロー検出

上記より「正の数＋負の数」または「負の数＋正の数」の場合、オーバーフローは発生しません。すなわち、ふたつの数値の符号が異なればオーバーフローが発生しません。

Ｄ＝Ｂ＋Ｃ を求めるとします。

オーバーフローの検出

オーバーフローの検出

ＢとＣの排他的論理和(Ｂ xor Ｃ)のMSB＝1ならば、異符号なのでオーバーフローは発生しません。

「正の数＋正の数」の場合、キャリー CYとＤの状態は「0|0・・・」か「0|1・・・」となり、後者は符号ビット(MSB)が「0」→「1」となり負の数となるのでオーバーフローしています。

「負の数＋負の数」の場合、キャリー CYとＤの状態は「1|0・・・」か「1|1・・・」となり、前者は符号ビット(MSB)が「1」→「0」となり正の数となるのでオーバーフローしています。

すなわち、ＣとＤの排他的論理和(Ｃ xor Ｄ)のMSB＝1の場合にオーバーフローが発生します。

整理すると、次のようになります。

(Ｂ xor Ｃ)のMSB＝0 かつ (Ｃ xor Ｄ)のMSB＝1の場合、オーバーフローが発生します。

i8080サチュレート加算コード

インテル8080マイクロプロセッサでオーバーフローを検出してサチュレート加算するコード(SADD8)を下記に示します。

レジスタＢとレジスタＣをサチュレート加算してレジスタＡに結果を求めます。

  
;========================================
;  Saturate Add A=B+C
;     (IN)     B  :  SIGNED BYTE DATA1
;     (IN)     C  :  SIGNED BYTE DATA2
;     (OUT)    A  :  SIGNED BYTE DATA1 + DATA2
;----------------------------------------
SADD8:
        MOV     A,B
        ADD     C
        MOV     D,A          ; D = B+C
;
        MOV     A,B
        XRA     C            ; B XOR C
        MOV     A,D          ; A = B+C
        RM                   ; IF BIT7=1 THEN DIFF SIGN (B,C)=(+,-)OR(-,+) NOT OVERFLOW
;                            ; IF BIT7=0 THEN SAME SIGN (B,C)=(+,+)OR(-,-) 
;
        XRA     C            ; D XOR C
        MOV     A,D          ; A = B+C
        RP                   ; IF BIT7=0 THEN SAME SIGN (D,C)=(+,+)OR(-,-) NOT OVERFLOW
;
        MOV     A,C
        ANA     A            ; A = C
        MVI     A,07FH
        RP                   ; IF BIT7=0 THEN + OVERFLOW (7F)
        INR     A            ; IF BIT7=1 THEN - OVERFLOW (80)
;
        RET

【SADD8 プログラム説明】

・D ← B + C を算出します
・Flag ← B xor Cを求め、A←D
・Sign Flag ONならば、returnします(RM) …BとCは異符号
・Flag ← D xor Cを求め、A←D
・Sign Flag OFFならば、returnします(RP) …DとCは同符号
・Flag ← Cを求め、A←07FH
・Sign Flag OFFならば、returnします(RP) …Cは正数 : オーバーフロー
・A←A+1 (080H)
・returnします …Cは負数 : オーバーフロー

サチュレート加算テストコード

SADD8をテストするコードを書きます。テストケースを下記に示します。

Ｂ Ｃ 期待値 備考
+100 +20 +120 + +
+100 +27 +127 + +
+100 +28 +127 + + OV
+100 +29 +127 + + OV
+100 -20 +80 + –
+100 -127 -27 + –
-100 +20 -80 – +
-100 +127 +27 – +
-100 -20 -120 – –
-100 -27 -127 – –
-100 -28 -128 – –
-100 -29 -128 – – OV
-100 -30 -128 – – OV

テストケースをDB(Define Byte)で定義します。DBは、正の数値しか定義できませんので、マイナスの数値は＋２５６して定義します。

     DB      0ffh , 100 ,   20     ,  120    ,00h ;  + +
     DB      0ffh , 100 , -127+256 , -27+256 ,00h ;  + -
  • 最初の0ffhは、FF=実行／00=停止のフラグ
  • 100は、数値Ｂ
  • 20は、数値Ｃ
  • 120は、数値Ｂ+数値Ｃの期待値
  • 00hは、計算結果を格納する領域

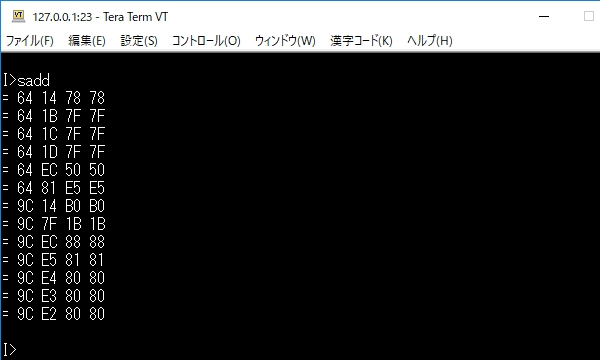
実行結果の確認のため、BとCと期待値と加算結果を16進でダンプします。期待値と加算結果が一致した場合は「=」、不一致の場合は「?」を表示します。

実行結果を下記に示します。

SADDの実行

SADDの実行

テストコードを下記に示します。

  

;---------------------------------
        ORG     0100h
START:
        LXI     H,CASE
;
LOOP:
        MOV     A,M         ; JUDGE
        ANA     A
        JZ      EXIT        ; 00 IS EXIT
;
        INX     H
        MOV     B,M         ; B LOAD
        INX     H
        MOV     C,M         ; C LOAD
        INX     H
        CALL    SADD8       ; A = B+C
        MOV     D,M         ; D LOAD (EXPECT)
        INX     H
        MOV     M,A         ; A STORE
        CMP     D     
        MVI     A,'='
        JZ      EQOK
        MVI     A,'?'
EQOK:
        DCX     H
        DCX     H
        DCX     H
        DCX     H
        MOV     M,A         ; STORE JUDGE
;
        MOV     A,M
        INX     H
        CALL    CONOUT       ; JUDGE
        MVI     A,' '
        CALL    CONOUT       ; SP
        MOV     A,M
        INX     H
        CALL    OUTHEX       ; B
        MOV     A,M
        INX     H
        CALL    OUTHEX       ; C
        MOV     A,M
        INX     H
        CALL    OUTHEX       ; EXPECT
        MOV     A,M
        INX     H
        CALL    OUTHEX       ; RESULT
        MVI     A,0Ah
        CALL    CONOUT       ; CR
;
        JMP     LOOP
;
EXIT:
        RET               ; return CP/M
;----------------------------------------
;
CASE:  
        DB      0ffh , 100 ,   20 ,  120 ,00h ;  + + 
        DB      0ffh , 100 ,   27 ,  127 ,00h ;  + + 
        DB      0ffh , 100 ,   28 ,  127 ,00h ;  + + OV
        DB      0ffh , 100 ,   29 ,  127 ,00h ;  + + OV
;
        DB      0ffh , 100 ,  -20+256 ,  80     ,00h ;  + - 
        DB      0ffh , 100 , -127+256 , -27+256 ,00h ;  + - 
;
        DB      0ffh ,-100+256 ,  20 ,  -80+256 ,00h ;  - + 
        DB      0ffh ,-100+256 , 127 ,   27     ,00h ;  - + 
;
        DB      0ffh ,-100+256 , -20+256 , -120+256 ,00h ;  - - 
        DB      0ffh ,-100+256 , -27+256 , -127+256 ,00h ;  - - 
        DB      0ffh ,-100+256 , -28+256 , -128+256 ,00h ;  - - 
        DB      0ffh ,-100+256 , -29+256 , -128+256 ,00h ;  - - OV
        DB      0ffh ,-100+256 , -30+256 , -128+256 ,00h ;  - - OV
;
        DB      00h
;
;==============================================================
BUFF:   DS      2
;
;========================================
; CONSOLE HEX OUTPUT From A-REG
;     (IN)     A  :  00-FF
;----------------------------------------
OUTHEX:
        PUSH   H
;
        LXI    H,BUFF
        CALL   CV8BIT
;
        LXI    H,BUFF
        MOV    A,M
        INX    H
        CALL   CONOUT
        MOV    A,M
        CALL   CONOUT
;
        MVI    A,' '
        CALL   CONOUT
;
        POP    H
        RET
;-----------------------------------------
BDOS    EQU    0005h
;
ASCA    EQU    'A'
ASC0    EQU    '0'
;========================================
;  Convert A-REG Value(00-FF) to HEX Char
;     (IN)     A  :  00-FF
;     (IN)     HL :  Store Address
;----------------------------------------
CV8BIT:
        MOV     B,A       ; A is CODE
        RRC
        RRC
        RRC
        RRC
        ANI     00Fh      ; A is Up  4bit
        CALL    CV4BIT
        MOV     M,A
        INX     H
        MOV     A,B       ; A is CODE
        ANI     00Fh      ; A is Lo  4bit
        CALL    CV4BIT
        MOV     M,A
        RET
;========================================
;  Convert A-REG Value(0-F) to HEX Char
;     (IN)     A :  Low 4bit 0-F
;     (OUT)    A :  HEX Char
;----------------------------------------
CV4BIT:
        CPI     0Ah
        JM      CNVH10
        ADI     ASCA-ASC0-10
CNVH10:
        ADI     ASC0           ; A is '0'-'9' 'A'-'F'
        RET
;========================================
; CONSOLE OUTPUT From A-REG
;     (IN)      A :  Console Output Char
;----------------------------------------
CONOUT:
        PUSH    H
        PUSH    D
        PUSH    B
;
        MVI     C,02H
        MOV     E,A
        CALL    BDOS
;
        POP     B
        POP     D
        POP     H
        RET
        END

最後に

インテル8080マイクロプロセッサで符号つき整数のサチュレート加算するコードを書きました。8080にはオーバーフローフラグがありませんので、ソフトでオーバーフロー検出するアルゴリズムを整理しました。

オーバーフローが発生する状況を整理すると、そんなに複雑ではありませんでした。