画像の膨張・収縮アルゴリズム

2017年8月、画像の膨張・収縮アルゴリズムについて調べました。
膨張・収縮アルゴリズムは画像処理の基本的な処理であり、「TI C64x DSPによる画像認識の最適化実装」で認識の前処理として組み込んでいました。

TI C64x DSPによる画像認識の最適化実装

---

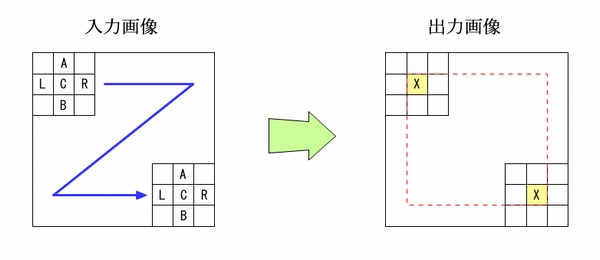
膨張・収縮アルゴリズムは、二値化した白黒の画像に対して 3×3画素のブロックをラスタスキャンして、注目画素(C:中央)とその周囲(A:上、B:下、L:左、R:右)の画素状態から中央の画素(X)を決定します。

• 膨張処理（Dilation）とは、注目画素の周辺に白い画素が１画素でもあれば白に置き換える処理です。
• 収縮処理（Erosion） とは、注目画素の周辺に黒い画素が１画素でもあれば黒に置き換える処理です。

3×3画素のブロックから中央の画素を決定しますので、出力画像の周囲画像(赤点線の外側)は算出できません。周囲画像を算出するために、画像の外にはみ出した画素を仮想的に周辺画素で補う方法があります。しかし、画像認識などでは周囲１画素は使用頻度が少ないことから、本説明では周囲画像は黒画像固定とします。

画像の膨張アルゴリズム

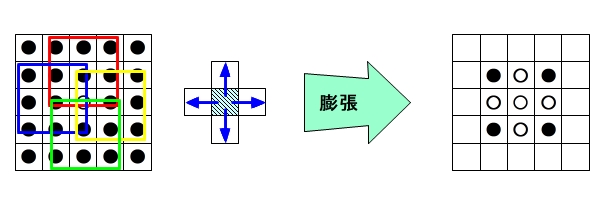
膨張アルゴリズムは、注目画素の周囲(上下左右)に白い画素が１画素でもあれば注目画素を白に置き換える処理です。

5×5の画像を例にします。

 

行－列	中央	上	下	左	右	結果
1－1	●	●	●	●	●	●
1－2	●	●	○	●	●	○
1－3	●	●	●	●	●	●
2－1	●	●	●	●	○	○
2－2	○	●	●	●	●	○
2－3	●	●	●	○	●	○
3－1	●	●	●	●	●	●
3－2	●	○	●	●	●	○
3－3	●	●	●	●	●	●

1－2(赤枠)、2－1(青枠)、2-3(黄色枠)、3－2(緑枠)の4つの画素を白色に置換します。

---

---

C++言語によるアルゴリズムコードを示します。

 

void Image_dilation( int iw ,int ih ,const unsigned char *pucSrc ,unsigned char *pucDst )
{
    for(int iy=1; iy<ih-1; iy++)
    {
        for(int ix=1; ix<iw-1; ix++)
        {
            unsigned char uc = pucSrc[ (iy+0)*iw + (ix+0) ];    // 中央
            unsigned char ua = pucSrc[ (iy-1)*iw + (ix+0) ];    // 上
            unsigned char ub = pucSrc[ (iy+1)*iw + (ix+0) ];    // 下
            unsigned char ul = pucSrc[ (iy+0)*iw + (ix-1) ];    // 左
            unsigned char ur = pucSrc[ (iy+0)*iw + (ix+1) ];    // 右
            //
            unsigned char ux =  0x00;
            if (uc != 0x00)   { ux = 0xFF; }
            if (ua != 0x00)   { ux = 0xFF; }
            if (ub != 0x00)   { ux = 0xFF; }
            if (ul != 0x00)   { ux = 0xFF; }
            if (ur != 0x00)   { ux = 0xFF; }
            //
            pucDst[ iy*iw + ix ] = ux;
        }
    }
}

画像の収縮アルゴリズム

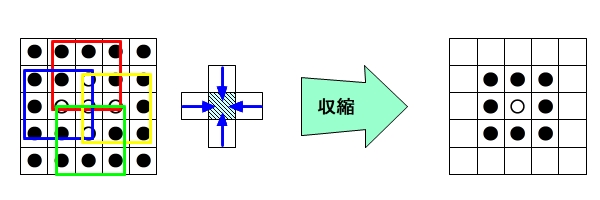
収縮アルゴリズムは、注目画素の周囲(上下左右)に黒い画素が１画素でもあれば注目画素を黒に置き換える処理です。

5×5の画像を例にします。

 

行－列	中央	上	下	左	右	結果
1－1	●	●	○	●	●	●
1－2	○	●	○	●	●	●
1－3	●	●	○	○	●	●
2－1	○	●	●	●	○	●
2－2	○	○	○	○	○	○
2－3	○	●	●	○	●	●
3－1	●	○	●	●	○	●
3－2	○	○	●	●	●	●
3－3	●	○	●	○	●	●

1－2(赤枠)、2－1(青枠)、2-3(黄色枠)、3－2(緑枠)の4つの画素を黒色に置換します。

---

---

C++言語によるアルゴリズムコードを示します。

 

void Image_erosion( int iw ,int ih ,const unsigned char *pucSrc ,unsigned char *pucDst )
{
    for(int iy=1; iy<ih-1; iy++)
    {
        for(int ix=1; ix<iw-1; ix++)
        {
            unsigned char uc = pucSrc[ (iy+0)*iw + (ix+0) ];    // 中央
            unsigned char ua = pucSrc[ (iy-1)*iw + (ix+0) ];    // 上
            unsigned char ub = pucSrc[ (iy+1)*iw + (ix+0) ];    // 下
            unsigned char ul = pucSrc[ (iy+0)*iw + (ix-1) ];    // 左
            unsigned char ur = pucSrc[ (iy+0)*iw + (ix+1) ];    // 右
            //
            unsigned char ux =  0xFF;
            if (uc != 0xFF)   { ux = 0x00; }
            if (ua != 0xFF)   { ux = 0x00; }
            if (ub != 0xFF)   { ux = 0x00; }
            if (ul != 0xFF)   { ux = 0x00; }
            if (ur != 0xFF)   { ux = 0x00; }
            //
            pucDst[ iy*iw + ix ] = ux;
        }
    }
}

収縮→膨張 オープニング（Opening）

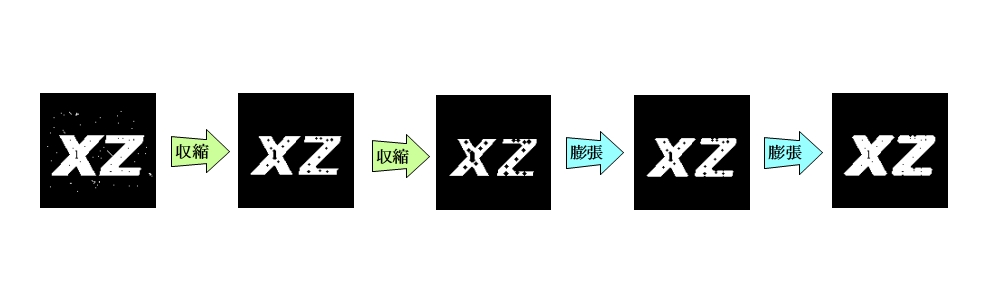
収縮を複数回実施した後に膨張を同じ回数実施する処理をオープニング（Opening）といいます。

収縮を２回実施後に膨張を２回実施した例を示します。

小さな白点のノイズを除去することができました。

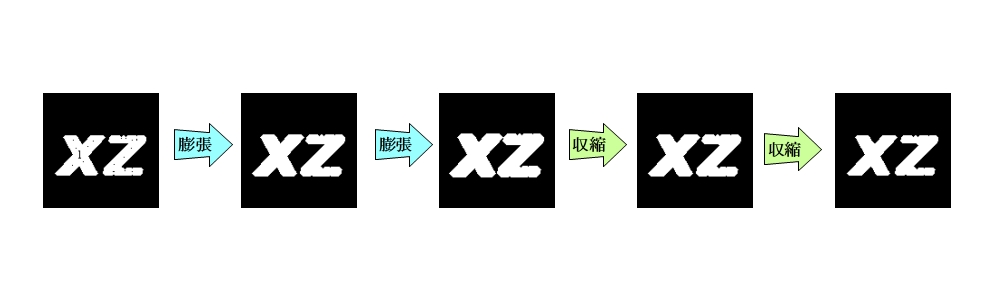
膨張→収縮 クロージング（Closing）

膨張を複数回実施した後に収縮を同じ回数実施する処理をクロージング（Closing）といいます。

膨張を２回実施後に収縮を２回実施した例を示します。

小さな黒点のノイズを除去することができました。

コードの重複について

膨張アルゴリズムと収縮アルゴリズムのコードを比べてみると、Y座標とX座標によるラスタスキャン・ループの部分は同じコードです。

注目画素とその周囲(上下左右)の画素状態から中央の画素を決定する部分が異なるだけです。

{
    for(int iy=1; iy<ih-1; iy++)
    {
        for(int ix=1; ix<iw-1; ix++)
        {
            unsigned char uc = pucSrc[ (iy+0)*iw + (ix+0) ];    // 中央
            unsigned char ua = pucSrc[ (iy-1)*iw + (ix+0) ];    // 上
            unsigned char ub = pucSrc[ (iy+1)*iw + (ix+0) ];    // 下
            unsigned char ul = pucSrc[ (iy+0)*iw + (ix-1) ];    // 左
            unsigned char ur = pucSrc[ (iy+0)*iw + (ix+1) ];    // 右
            //
            unsigned char ux =  ・・・　
            ■
            ■　 異なるコード部分
            ■
            //
            pucDst[ iy*iw + ix ] = ux;
        }
    }
}

この膨張・収縮アルゴリズムのコードの場合は、簡単なコードなので重複していることは気になりません。しかし、もう少し複雑なコードだった場合はどうでしょうか？両者の重複コードをコピペで保守していくでしょうか？

あるプロセッサ向けに最適化実装する過程でコードをリファクタリングしていく場合に、何度もコピペしますか？何か工夫したくなりませんか？

このあたりのことを考えてみたいと思います。