コラム「北斗七星」

2024年6月13日の公明新聞のコラム「北斗七星」を読んで、好奇心を持って行動したいと思いました。

コラム「北斗七星」2024.6.13

インターネットで検索していて気になる本を見つけた。
タイトルは『小学生が99×99までスイスイ暗算できる最強ドリル』(岩波邦明著、小学館)。
説明文を読んで「そんなことが可能?」と思った

（･･･ 中略 ･･･）

全ての掛け算が一つの方法で解ける「あゆみ算」という暗算法が紹介されている。

（･･･ 中略 ･･･）

「思いがけないものの発見。運よく発見したもの」
の意味で使われるセレンディピティという言葉がある。
デジタルと現実の世界の中で、ふとした偶然が重なり、
新しい状況が生まれる。
好奇心を持って行動するからこそ、予期せぬ幸運に出合えるのだろう。

（歩）

あゆみ算とは

コラムで紹介していた「小学生が99×99までスイスイ暗算できる最強ドリル」を少し調べてみました。

「あゆみ算」とは、最先端のAIを学ぶ現役スタンフォード生の岩波邦明医師が独自に考案した画期的な暗算法のことです。

人間の脳には、ワーキングメモリという情報を一時的に記憶・処理する部分がありますが、覚えていられる数字の桁数がとても少ないのです。従って、なるべく少ない桁数でワーキングメモリをうまく活用して、計算するときに頭の中で扱う数字の数を減らすことで、2桁×2桁の暗算を簡便化しているとのことです。

何年も前にブームになったインド式暗算とは、異なる手法のようです。

---

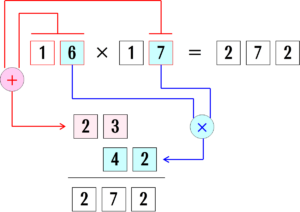
「16×17＝272」の計算例が書いてありました。

---

1. たす　16＋7＝23
2. かけ　6×7＝42
3. まとめ 230＋42＝272

式を展開してみると、確かにあってますね。

16×17＝16×(10＋7)＝16×10＋16×7＝16×10＋(10＋6)×7＝16×10＋10×7＋6×7＝(16＋7)×10＋(6×7)＝230＋42＝272

まあ、私にはそんなに便利には思いませんでしたけど。2桁×2桁の暗算なんて、そんなにすることは無いかと思います。

好奇心から偶然の出会い

このコラムが私の気を引いたのは、「思いがけないものの発見。運よく発見したもの」の意味で使われるセレンディピティという言葉です。

『好奇心を持って行動するからこそ、予期せぬ幸運に出合えるのだろう』

 

ウェブサイト『ある計算機屋さんの手帳』の目的が、偶然の出会いであるセレンディピティ（serendipity）を目指しているからです。

本屋で何かを探しているときに、探しているものとは別の価値があるものを偶然発見したことはありませんか？

その昔、「bit」（目次）という技術情報誌がありました。
この雑誌を読んでいると、無数の「点」だった技術同士がつながり「線」となりさらに「面」となり技術の理解を深くしてくれました。
また、素晴らしい技術に偶然に出会ったり、予想外のものを発見したりすることが多く、計算機屋さんとして多くのことを学びました。

---

『ある計算機屋さんの手帳』ウェブサイトもそんな偶然の発見があることを期待しています。

好奇心を持って挑戦する

2024年6月6日にNHKで『タイム・トラベラー』の一部が紹介されていました。
1972年に放送された懐かしいドラマです。

この放送を見て、もしもタイムトラベルできたら「どの時代のどの場所」へ行きたいか考えてみました。

---

〝昭和49年の京都へ行って学生時代の自分に会いたい！〟

そして、『しっかりと勉強せよ。経験はきっと役に立つのでいろいろと挑戦せよ！』と言いたい。

---

技術者人生でいろいろな分岐点がありましたが、自分の選んだ道に間違いはありませんでした。
そして、経験したことがどこかでつながって役に立っています。
経験を大切にして全力で挑戦すれば道は開けるものです。

この先、好奇心を持っていろいろ挑戦して、経験を重ねていきたいとあらためて思いました。